Dmitry Vasilenko, ingeniero senior de aplicaciones de Arrow Electronics.
Modelo mecánico de un acelerómetro MEMS
Los sistemas micromecánicos (MEMS) se han vuelto muy comunes en nuestra vida cotidiana, incluyendo una aplicación tan popular como la medición de la aceleración realizada por un acelerómetro. El principio de funcionamiento de un acelerómetro se muestra en la Fig. 1. El fundamentode un sensor de este tipo es una masa móvil m, fijada sobre suspensiones con un coeficiente de elasticidad k. Los condensadores con placas móviles están conectados a la masa y al cuerpo del sistema en paralelo a estas suspensiones.
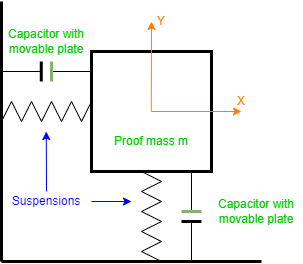
Fig. 1 Principio de funcionamiento del acelerómetro de 2 ejes.
El desplazamiento de la masa según la ley de Hooke es proporcional a su aceleración. En caso de pequeños desplazamientos de una masa, se observa una dependencia lineal entre este desplazamiento y la tensión en el circuito puente, combinado a partir de 2 condensadores con placas móviles. Por lo tanto, el modelo mecánico de un acelerómetro sigue las reglas de las oscilaciones forzadas y se describe mediante la fórmula:
![]()
La frecuencia de oscilación natural (o frecuencia de resonancia) y el factor Q se determinan mediante las fórmulas:

Así, la función de transferencia en la transformada de Laplace tendrá el siguiente aspecto:

En algunos acelerómetros con salida analógica se incorpora un filtro paso bajo adicional para atenuar la ganancia en la frecuencia de resonancia. Con esta finalidad, la función de transferencia original se multiplica por un término de filtro paso bajo con una frecuencia de corte ωC:
![]()
En el análisis de un sistema mecánico es habitual utilizar la analogía de un filtro LRC; véase un ejemplo en [2]. En este caso, la fórmula de la transformada de Laplace y las dependencias entre la frecuencia natural ω0 y el factor Q por un lado, y los parámetros del filtro LRC por otro, se muestran en las fórmulas (6):
![]()
Modelado del acelerómetro MEMS en LTSpice
Es posible modelar el acelerómetro MEMS utilizando la transformada funcional de Laplace de esta herramienta de simulación. Para ello, se puede emplear una fuente de tensión controlada por tensión (prefijo B de SPICE) y añadir la función Laplace en el atributo Value2 (Fig. 2).
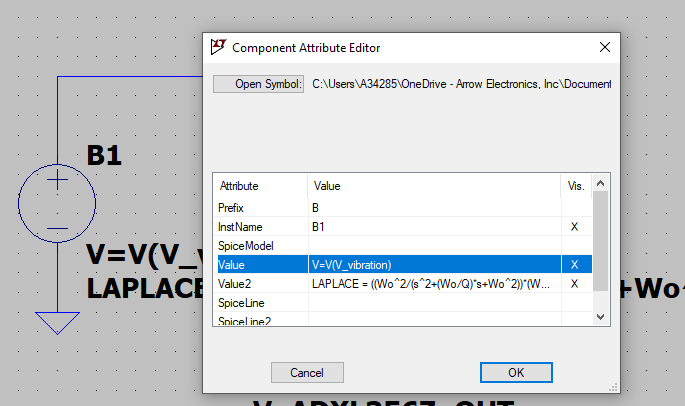
Fig. 2 Inserción de la fórmula de Laplace en el atributo Value2 en una fuente de tensión controlada por tensión.
El modelo del acelerómetro ADXL356, con sus parámetros de transformada de Laplace, se muestra en la Fig. 3.

Fig. 3 Modelo del acelerómetro ADXL365 con los parámetros de los ejes X e Y.
La respuesta de la frecuencia de este circuito concuerda bien con la hoja de datos del proveedor del ADXL365 (véase [4]). El resultado de la simulación a escala logarítmica se muestra en la Fig. 4:
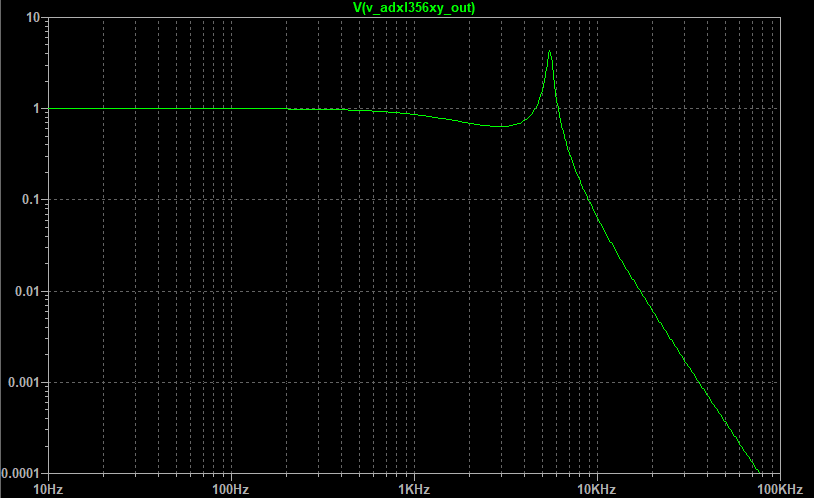
Fig. 4 Respuesta de la frecuencia del modelo ADXL356XY, buena concordancia con la hoja de datos del acelerómetro.
Los parámetros de la función de Laplace se pueden calcular para diferentes acelerómetros. Encontrará enumerado un resumen de algunos sensores de Analog Devices en la Tabla. 1:
| Nombre del acelerómetro | Wo | Q | Wc |
| ADXL356 (ejes X e Y) | 34562 | 17 | 9426 |
| ADXL356 (eje Z) | 32656 | 5 | 9426 |
| ADXL1001/2 | 131880 | 4 | No aplicable |
| ADXL1004 | 282600 | 4 | No aplicable |
Tabla. 1 Funcionamiento de la transformada de Laplace para distintos tipos de acelerómetros.
Modelado de la cadena de señal de sensores vibratorios.
El modelo de sensor vibratorio comentado puede utilizarse para una evaluación completa de una cadena de señal combinada. Esta cadena de señal incluye un acelerómetro y un filtro analógico utilizado a la salida del sensor para conectarlo al resto del sistema (normalmente con un ADC). En un circuito de filtro analógico es habitual utilizar un amplificador operacional de bajo ruido (por ejemplo, ADA4805/07). En este caso, dicho amplificador operacional suele utilizarse como filtro paso bajo. Esta implementación puede ayudar a reducir un valor de pico de resonancia y ampliar el rango de mediciones espectrales de vibración (en un rango de 3 dB). Encontrará un ejemplo del modelo de acelerómetro con un filtro paso bajo basado en un amplificador operacional en la Fig. 5. Además, el resultado del modelado confirma un incremento del rango de medición a un valor adicional dentro de los 3 dB, véase Fig. 6.

Fig. 5 Modelo del acelerómetro ADXL1002 utilizando un búfer para modelar una cadena de señal combinada.
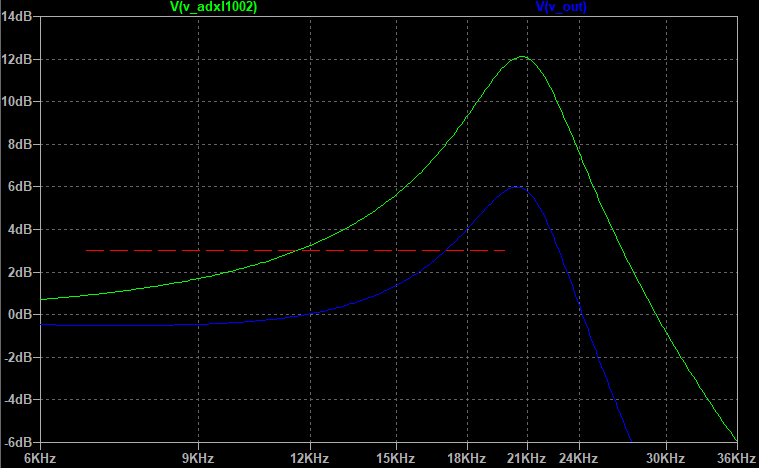
Fig. 6 El filtro paso bajo permite incrementar el rango de medición del sistema de sensores combinados, mientras que el punto de 3 dB desplaza la frecuencia de corte de 11 kHz a 17 kHz.
Esta técnica permite, adicionalmente, estimar el comportamiento de ruido del sistema. Para realizar dicho cálculo, se puede utilizar el algoritmo descrito en [3]. Para una estimación aproximada, se considera que el ruido del acelerómetro MEMS tiene una densidad espectral uniforme. La base de ruido espectral ADXL1002 se estima en 25 ug/. Con una tensión de alimentación del sensor de 5V, esta densidad espectral se expresará con un ruido de tensión de nivel 1,25 uV/. Para modelar este ruido uniforme, se puede utilizar una resistencia con un valor R=9002 ohmios y una fuente de tensión controlada por tensión con una ganancia de 1000, véase Fig. 7.
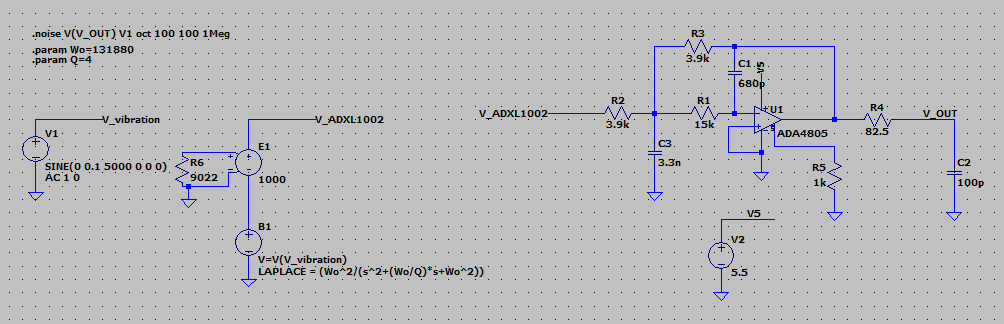
Fig. 7 Adición de una fuente de ruido a un nivel de 25 ug/.
El espectro de ruido calculado muestra que el ruido del acelerómetro dominará a bajas frecuencias y el circuito de amplificación a altas frecuencias, véase Fig. 8.

Fig. 8 Ruido espectral en la salida del acelerómetro.
Resumen
Es posible simular un acelerómetro MEMS con salida analógica en LTspice utilizando la funcionalidad de la transformada de Laplace. Los cálculos en el simulador permiten evaluar y optimizar el circuito de la cadena de señal analógica, incluyendo sus características de ruido. Este cálculo ofrece una elección óptima del circuito amplificador, permitiendo así ampliar el rango de medición del acelerómetro MEMS y acercarse a las características de un piezosensor de mayor coste.








